B-tree
B树的出现是为了弥合不同的存储级别之间的访问速度上的巨大差异,实现高效的 I/O。平衡二叉树的查找效率是非常高的,并可以通过降低树的深度来提高查找的效率。但是当数据量非常大,树的存储的元素数量是有限的,这样会导致二叉查找树结构由于树的深度过大而造成磁盘I/O读写过于频繁,进而导致查询效率低下。另外数据量过大会导致内存空间不够容纳平衡二叉树所有节点的情况。B树是解决这个问题的很好的结构
B树又称多路平衡查找树,B树中所有节点的孩子节点数的最大值称为B树的阶。
一颗m阶的B树定义如下:
- 每个节点最多有m个子树
- 每个节点最多有m-1个关键字
- 根节点最少有1个关键字
- 非根节点至少有Math.ceil(m/2)-1个关键字
- 所有叶子节点都位于同一层,或者说根节点到每个叶子节点的长度都相同
- 每个节点中的关键字都按照从小到大的顺序排列,每个关键字的左子树中的所有关键字都小于它,而右子树中的所有关键字都大于它
什么是B树的阶
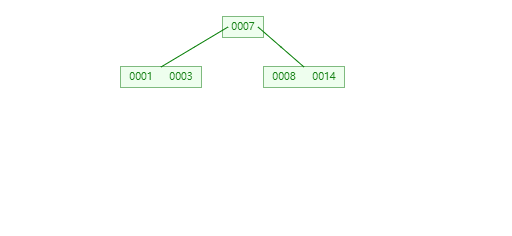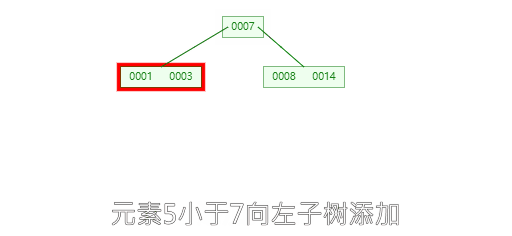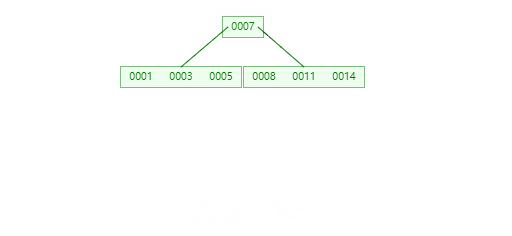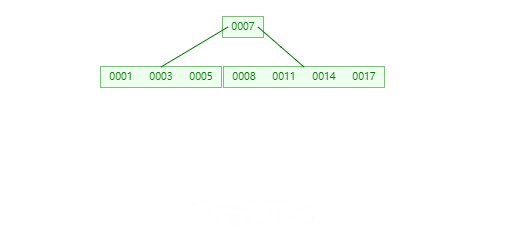
B树中一个节点的子节点数目的最大值,用m表示,假如最大值为10,则为10阶,如图:
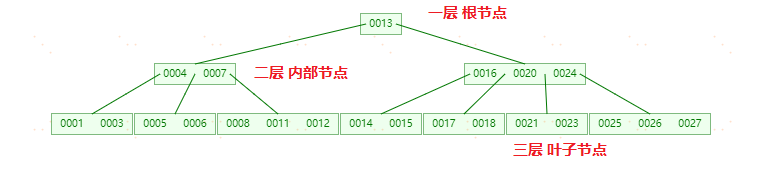
所有节点中,节点[13,16,19]拥有的子节点数目最多(4个子节点),所有可以定义上面的图片为4阶B树。
B-tree插入
针对m阶高度h的B树,插入一个元素是,首先在B树中是否存在,如果不存在,即在叶子节点处结束,然后再叶子节点中插入该新的元素。
插入规则:
- 若该节点元素个数小于m-1,直接插入
- 若该节点元素个数等于m-1,引起节点分裂;以该节点中间元素为分界,取中间元素(偶数个数,中间两个随机选取)插入到父节点中;
- 重复上面动作,直到所有节点符合B树的规则;最坏的情况一直分裂到根节点,生成新的根节点,高度增加1;
上面的规则是插入动作的核心,接下来以5阶树为例,详细讲解插入的动作:
下面演示下列数字的插入5阶B-tree树步骤(观看网站):
插入 1 ,3,7,14 如下图:

**插入8时,**此时根节点元素个数为5,不符合1<=根节点元素个数<=m-1,提取中间节点7进行分裂。

插入5,11,17时不需要任何分裂操作
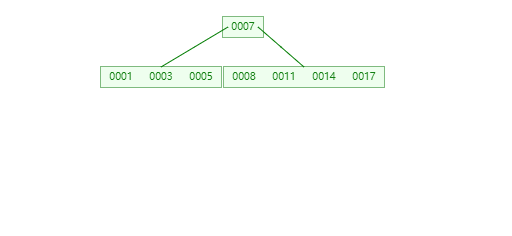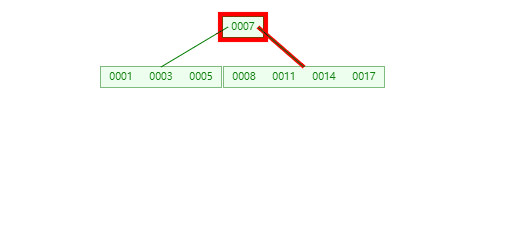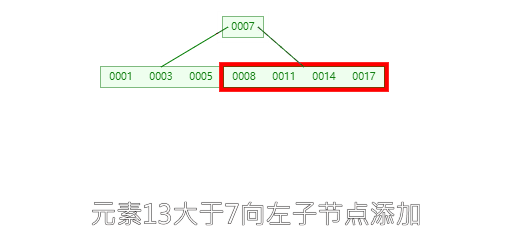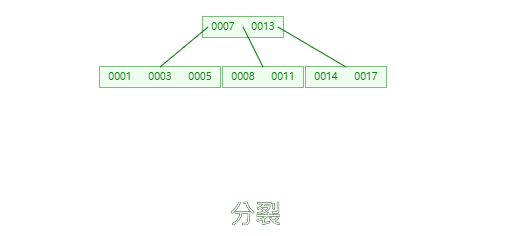
**插入元素 13 ,**由于13大于根节点7,向右子节点添加,又由于右节点已经有8,11,14,17四个节点,添加13就要进行分裂。提取中间元素13,插入到父节点中,插入过程如下图:
插入元素6,12,20,23时,不需要进行分裂
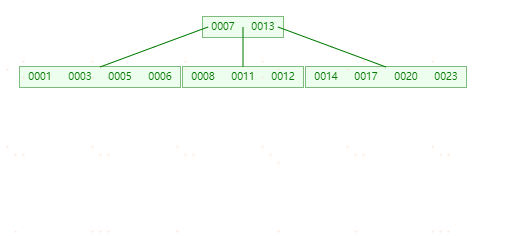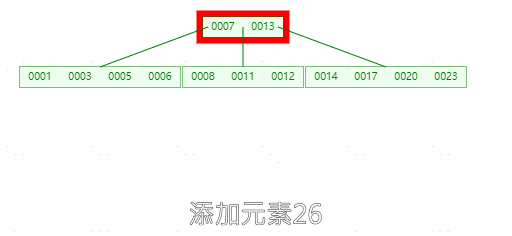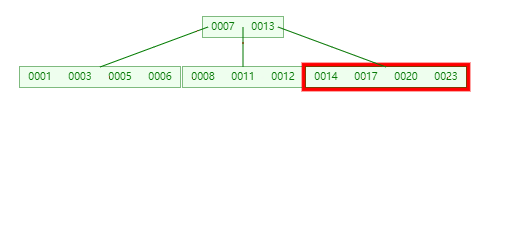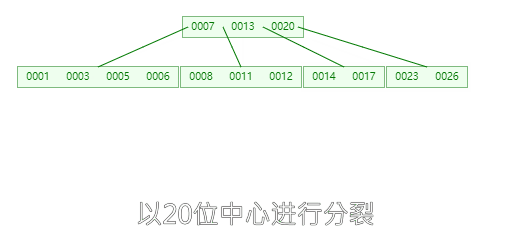
**插入26时,**26大于13应该添加到最右的叶子节点中,由于最右的叶子节点【14,17,20,23】空间已经满了,要进行分裂。
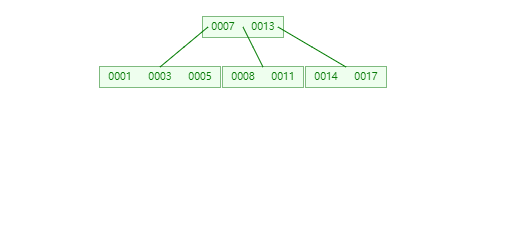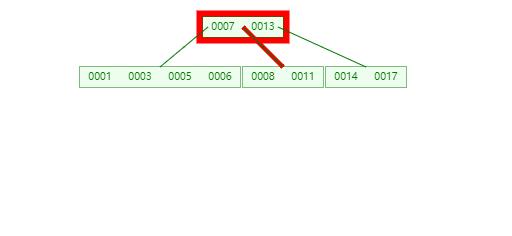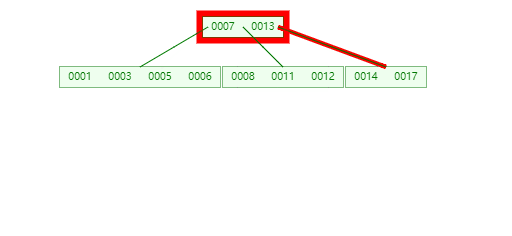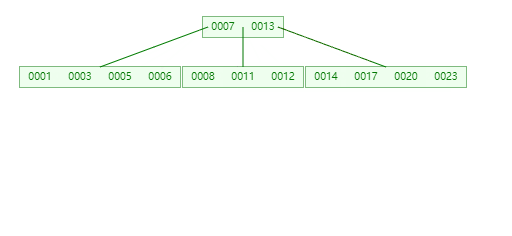
**插入4时,**导致最左边叶子节点进行分裂 【1,3,5,6】
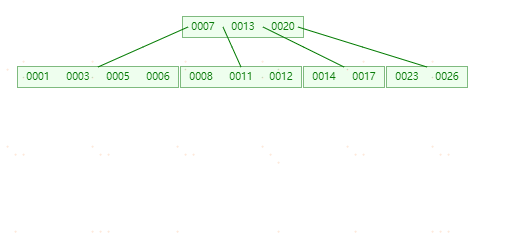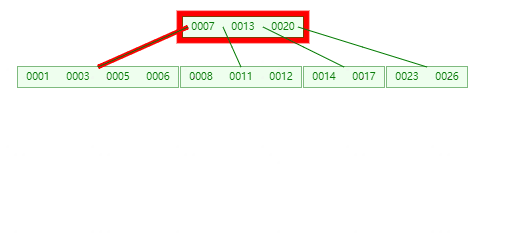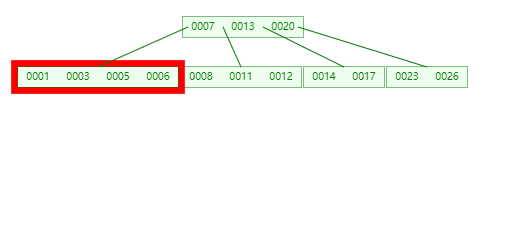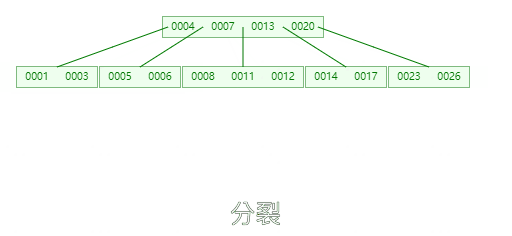
插入24,25时不进行分裂
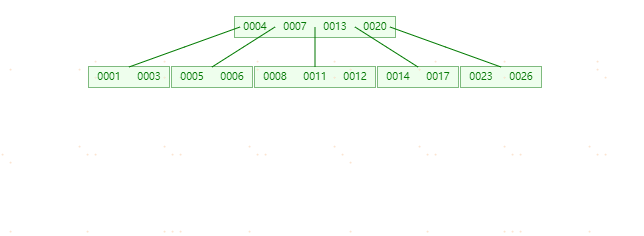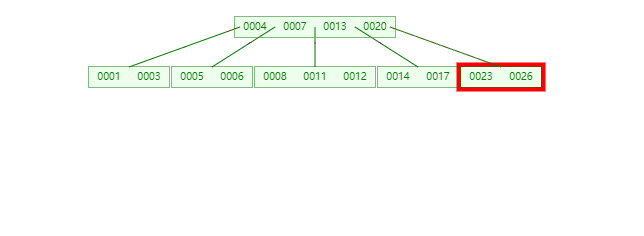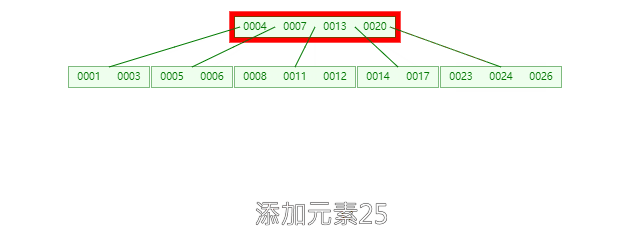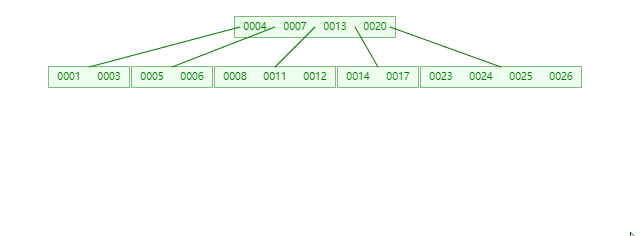
**插入21时,**含有【23,24,25,26】的节点需要分裂,把中间元素24上移到父节点中,但是父节点中空间已经满了,所以也要进行分裂,将父节点的中间元素【13】上移到形成新的根节点。 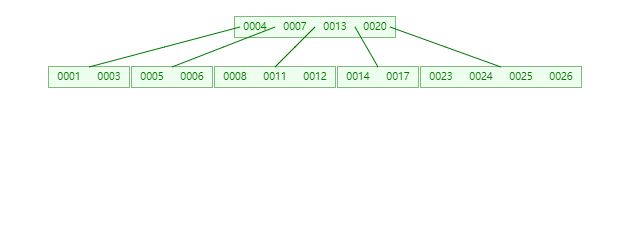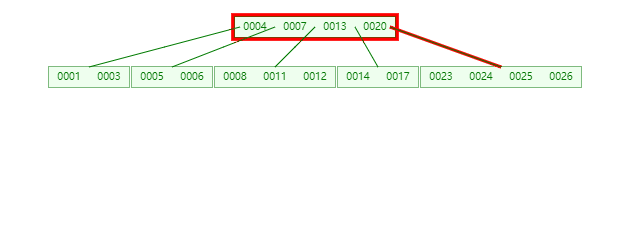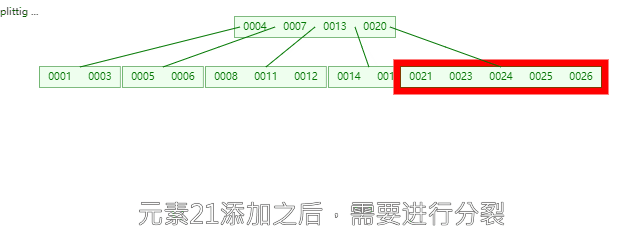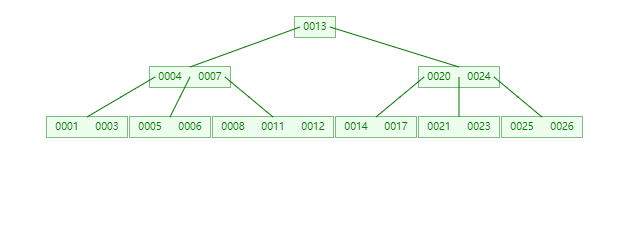
插入元素27不进行任何分裂
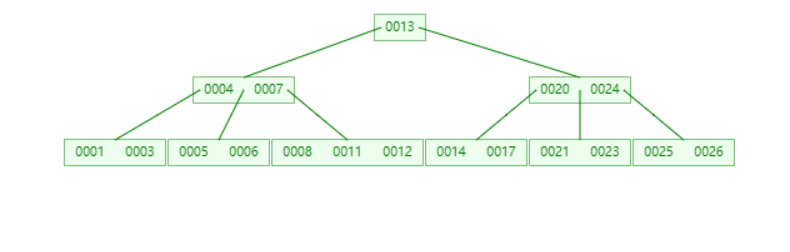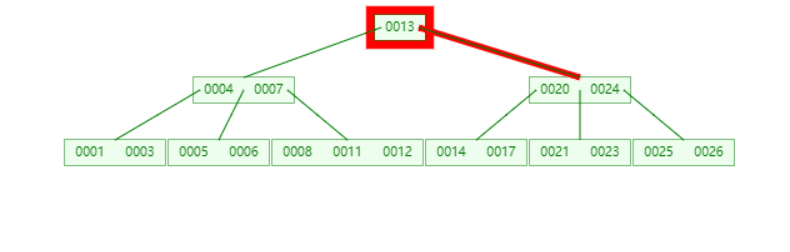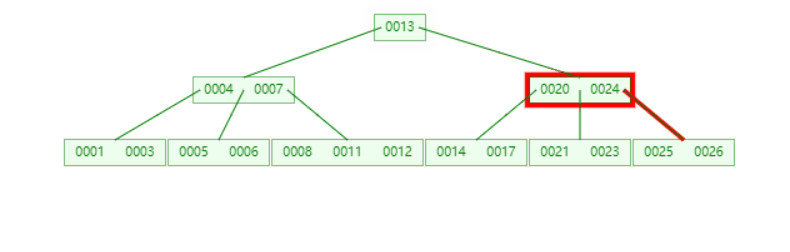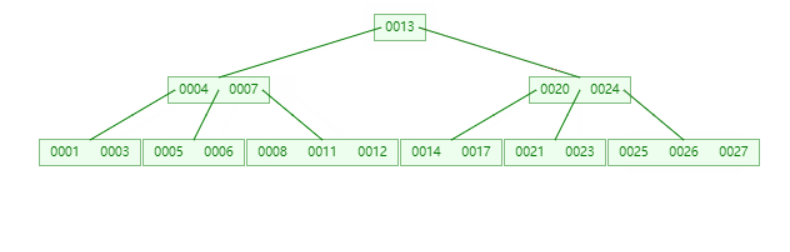
插入元素15,16不进行任何分裂
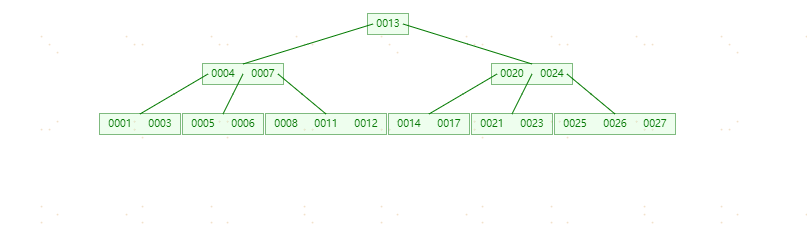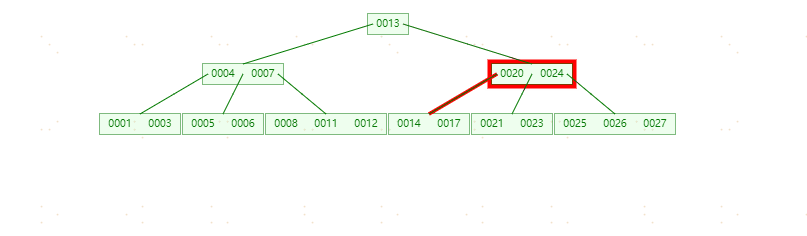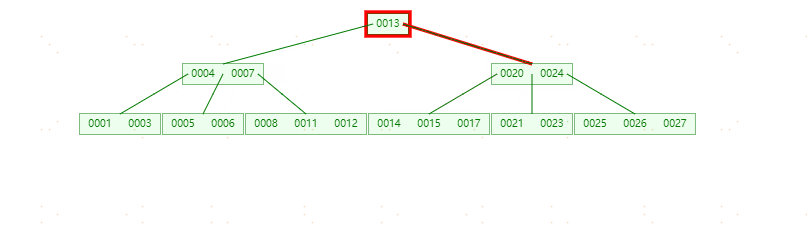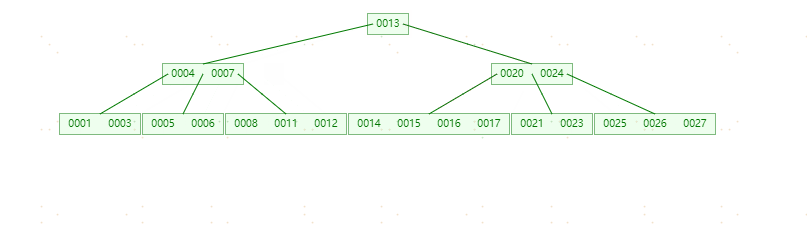
插入元素18分裂

总结B-tree为:
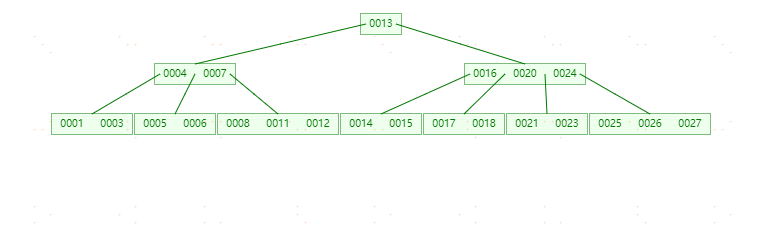
B-tree删除
首先查找B树中需删除的元素,如果该元素在B树中存在,则将该元素在其节点中进行删除;
删除步骤如下:
-
删除该元素后,首先判断该元素是否有左右孩子节点,如果有,则上移孩子节点中的某相近元素(“左孩子最右边的节点”或“右孩子最左边的节点”)到父节点中(左右孩子节点都可以,如果上移左孩子节点发现左节点个数少于Math.ceil(m/2)-1则上移右孩子节点),然后是移动之后的情况;如果没有,直接删除。
-
某节点中元素数目小于(m/2)-1,(m/2)向上取整,则需要看其某相邻兄弟节点是否丰满;
-
如果丰满(节点中元素个数大于(m/2)-1),则向父节点借一个元素来满足条件;
-
如果其相邻兄弟都不丰满,即其节点数目等于(m/2)-1,则该节点与其相邻的某一兄弟节点进行“合并”成一个节点。合并步骤:首先移动父节点中的元素(该元素在两个需要合并的两个节点元素之间)下移到其子节点中,然后将这两个节点进行合并并成一个节点。;
下面我们以上5阶B树为例来看一下删除的动作:
【1,3,7,14,8,5,11,17,13,6,12,20,23,26,4,24,25,21,27,15,16,18】

关键要领,元素个数小于2 【(m-1)/2-1】就合并,大于 4 【m-1】就分裂
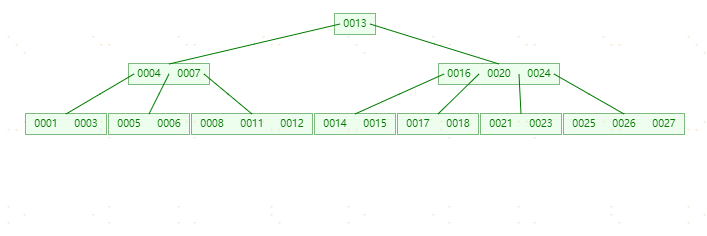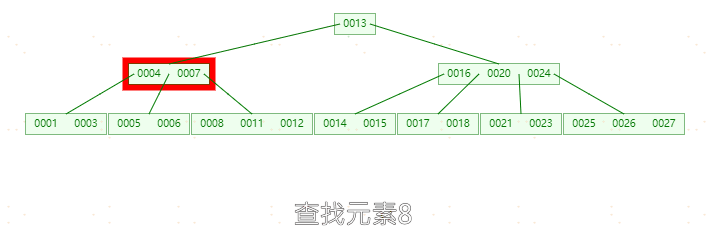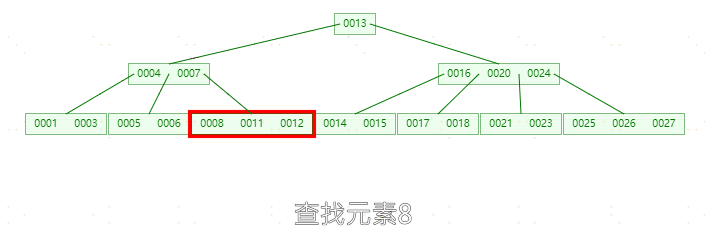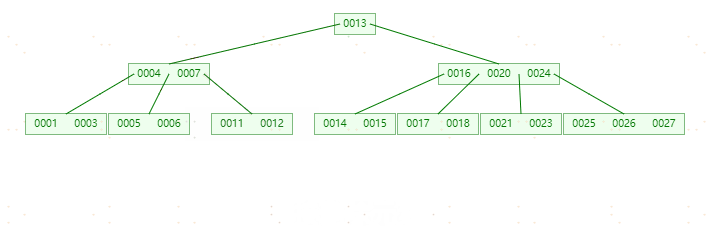
**删除元素8,**首先查找8的位置,发现8在【8,11,12】叶子节点处,删除8后该叶子节点元素个数为2,符合B树规则,直接删除。
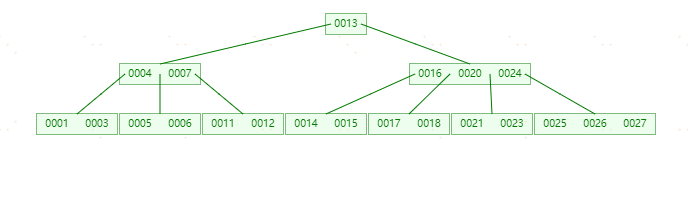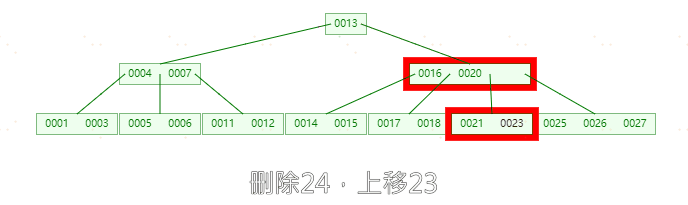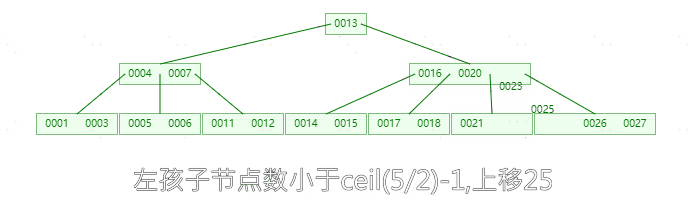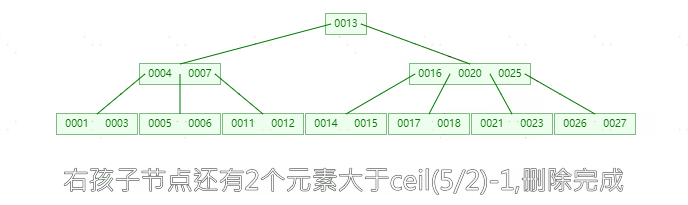
**删除元素24,**因为24在中间节点中,删除24之后,左孩子节点23上移,发现左孩子节点只剩一个元素(小于两个元素),而右孩子节点个数为3(大于ceil(5/2)-1),上移右孩子25,此时左右孩子节点都剩两个元素(不小于 ceil(5/2)-1),删除完成
**删除元素25,**删除25节点之后,左孩子节点23上移,发现左孩子节点只剩一个元素(小于ceil(5/2)-1),而右孩子节点个数为2(不大于ceil(5/2)-1)。则进行合并。

**删除元素5,**因为5所在的节点数目刚好满足(ceil(5/2)-1),而相邻的兄弟节点个数都为2(等于ceil(5/2)-1);则进行合并,合并之后如下图:
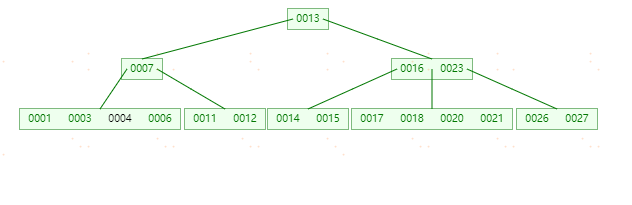
但是此时删除操作还没哟结束,此时元素7所在的节点个数为一(不符合非根节点元素K必须满足于ceil(5/2)-1=<K<=m-1 也就是2<=k<=4的定义);如果这个问题节点的相邻兄弟比较丰满,则可以向父节点借一个元素,但此时兄弟节点元素个数刚好为两个,只能进行合并。而根结点中的唯一元素【13】下移到子结点,这样,树的高度减少一层。
B+tree
B+tree是B-tree的变种,有着比B-tree更高的查询性能:
- 有m个子树的节点包含有m个元素(B-tree是m-1)
- 只有叶子结点保存数据,其他节点都只用于索引
- 根节点和所有分支节点都同时存在于叶子结点中,在子节点元素中是最大或者最小的
- 叶子节点会包含所有的关键字,以及指向数据记录的指针,并且叶子节点本身是根据关键字的从小到大顺序链接
B+tree插入
B+tree的插入必须保证插入后叶子节点中的记录依然排序,同时需要考虑插入到B+tree的三种情况,每种情况都可能会导致不同的插入算法 。
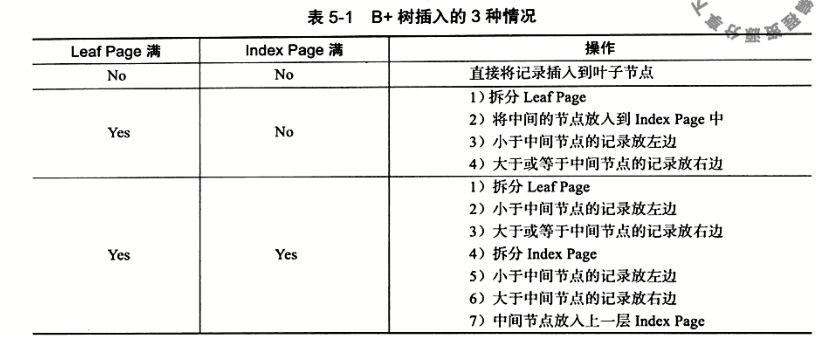
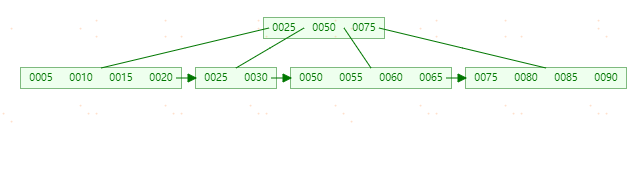
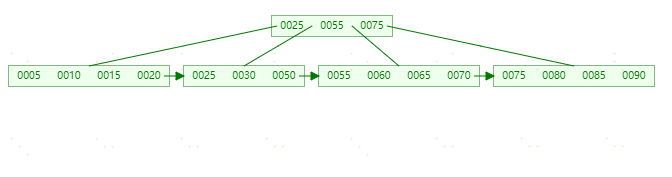
依次插入【5,10,25,30,50,55,75,80,85,90,15,20,60,65】

最后结果为下图:
**插入70,**此时原先的Leaf Page已经满了,但是Index Page还没有满,符合上表中的第二种情况,这时插入Leaf Page后的情况为 【50,55,60,65,70】,并根据中间的60来拆分叶子节点。
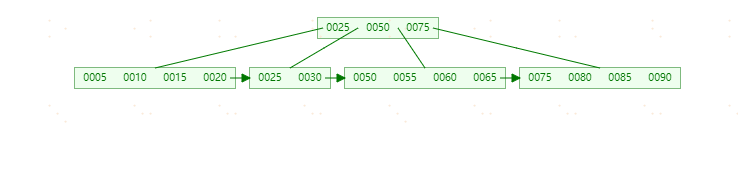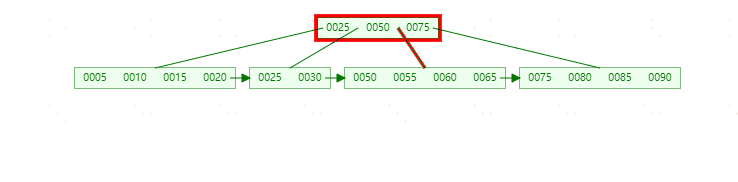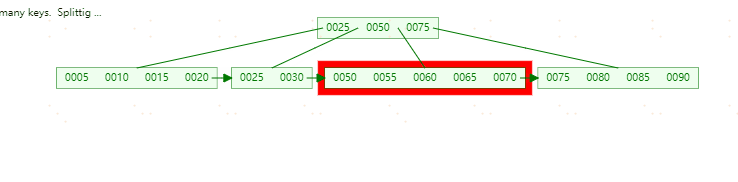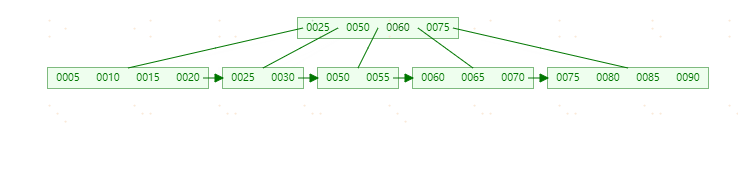
**插入95,**这时符合上表中第三种情况,即Leaf Page和Index Page都满了,这时需要做两次拆分。
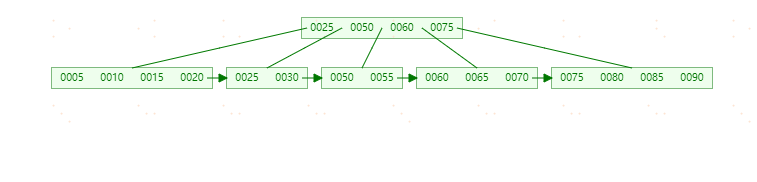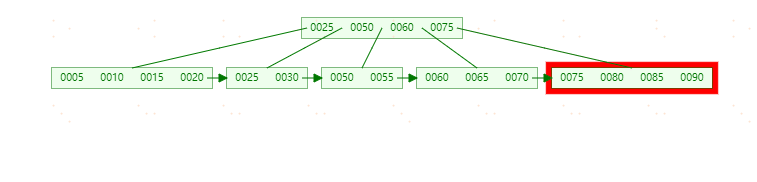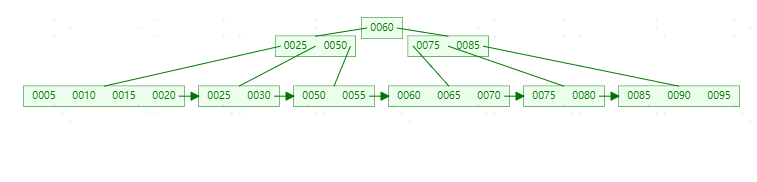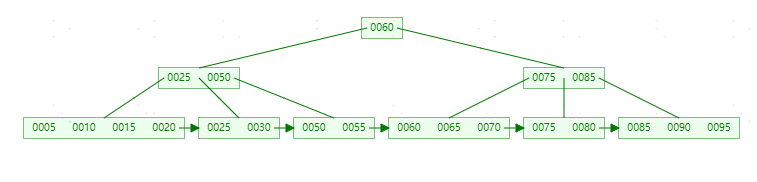
最终结构如下图:
可以看到,不管怎么变化,B+tree总是会保持平衡。但是为了保持平衡对于新插入的键值可能需要做大量的拆分页操作。
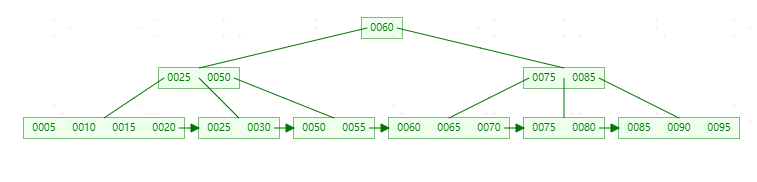
因为B+tree树结构主要用于磁盘,也的拆分意味着磁盘的操作,所以应该在有可能的情况下尽量减少也的拆分操作。因此,B+树同样提供了类似于平衡二叉树的旋转(Rotation)功能。旋转发生在Leaf Page已经满,但是其左右兄弟节点没有满的情况下。这时B+tree并不急于去做拆分也的操作,而是将记录移到所在页的兄弟节点上。因此再来看插入70的情况,若插入70,其实B+tree并不急于去拆分叶子节点,而是去做旋转操作,得到如下图:
插入70前
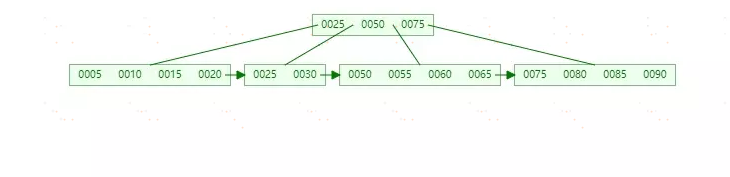
做拆分
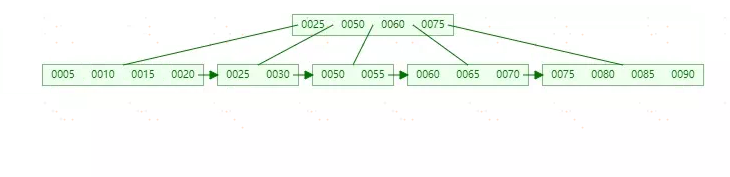
做旋转
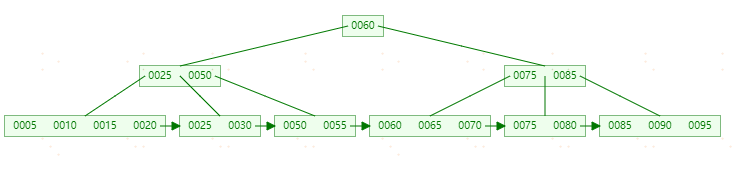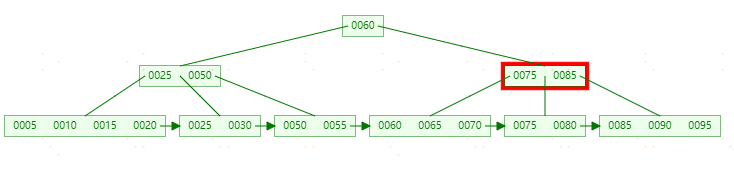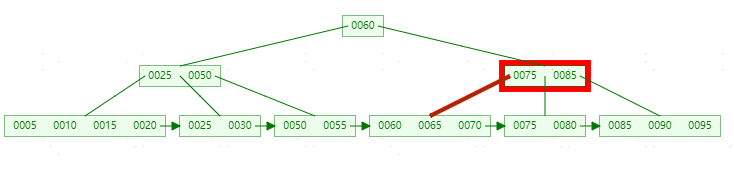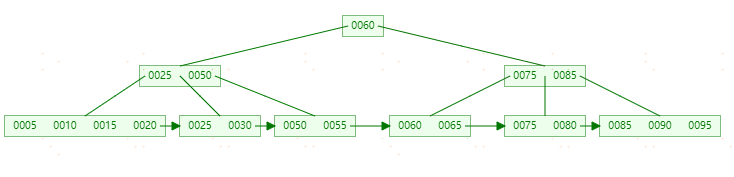
B+tree删除操作
B+tree树使用填充因子(fill factor)来控制树的删除变化。50%即(m/2)是填充因子可设的最小值。


**删除元素70,**该记录符合上表中第一种情况,可以直接删除
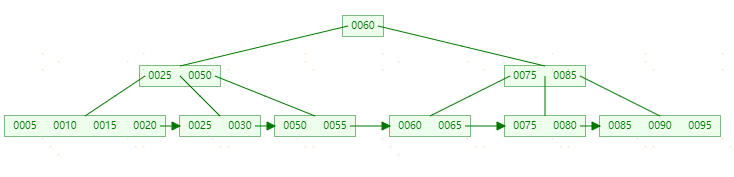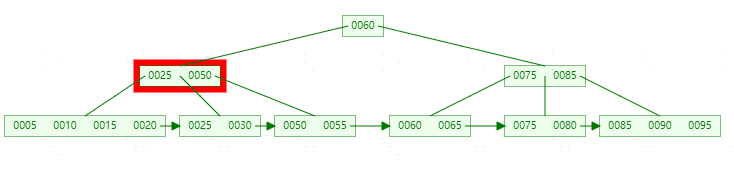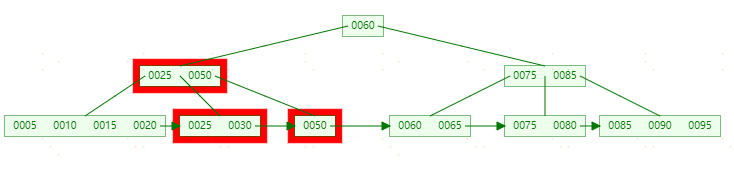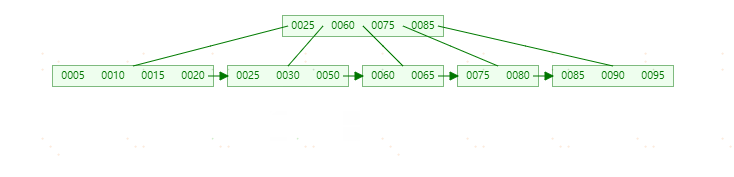
**删除55,**首先【50,55】节点只剩50,需要和【25,30】节点进行合并(合并规则和B-tree一样)。此时图如下:
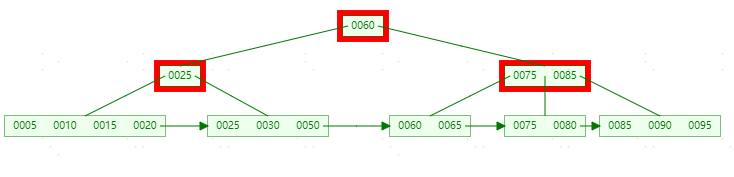
这个时候删除还没有结束,由于【25】节点只剩一个元素,需要和右节点进行合并。最终过程如下:
删除80,此时符合上表中第二种情况:

最终如下图:


