多因子试验

632 05-31

参考书
C.F.Jeff Wu and M.Hanmada (2009). Experiments: Planning, Analysis, and Parameter Design Optimization (2nd Edition). John Wiley & Sons.
方开泰，刘民千，周永道(2011). 试验设计与建模. 高等教育出版社.
Box, G.E.P., Hunter, J.S. and Hunter, W.G.(2005). Statistics for Experimenters: Design, Innovation, and Discovery(2nd ed), John Wiley & Sons).

配对比较试验：区组=2 的随机化区组
随机化区组设计
拉丁方设计：2区组1处理
希腊拉丁方设计
平衡不完全区组设计

一、配对比较试验
配对比较可以消除不同样品间的影响
例子：双胞胎，左右眼，左右手，左右身……（实际试验中能配对出现的）

例1：测量污水氯气含量，两种方法（MSI 和 SIB），测定精度上是否有差别？

sample	MSI	SIB	di
1	0.39	0.36	-0.03
2	0.84	1.35	0.51
3	1.76	2.56	0.80
4	3.35	3.92	0.57
5	1.69	5.35	0.66
6	7.70	8.33	0.63
7	10.52	10.70	0.18
8	10.92	10.91	-0.01

二、随机化区组设计

例2：预测钢梁剪切强度，b个区组，每个区组有k个单元，处理的个数N=bk。

钢梁	处理1	处理2	处理3	处理4
S1/1	0.772	1.186	1.061	1.025
S2/1	0.744	1.151	0.992	0.905
S3/1	0.767	1.322	1.063	0.930
S4/1	0.745	1.339	1.062	0.899
S5/1	0.725	1.200	1.065	0.871
S1/2	0.844	1.402	1.178	1.004
S2/2	0.831	1.365	1.037	0.853
S3/2	0.867	1.537	1.086	0.858
S4/2	0.859	1.559	1.052	0.805

三、拉丁方设计

拉丁方：由拉丁字母组合成的矩阵，字母每行每列均出现一次

例3：考虑塑料纤维的耐磨性
两个阻滞因素：1实验的四个位置；2四种测量的时间安排

	1	2	3	4
1	235	236	218	268
2	251	241	227	229
3	234	273	274	226
4	195	270	230	225

模型：
方差分解：
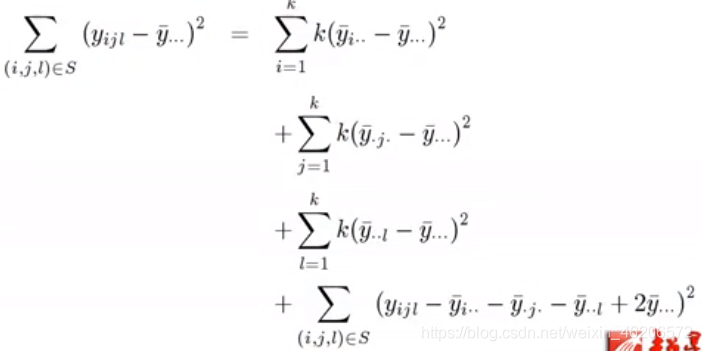
方差分析表

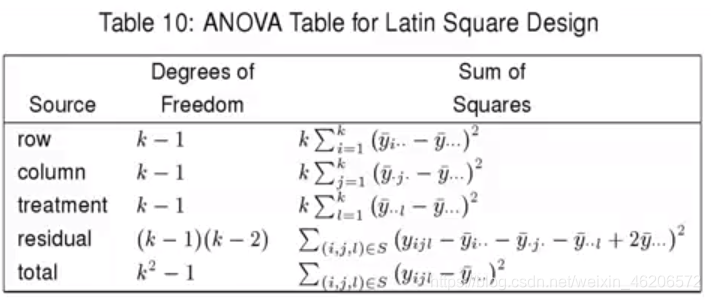
例4：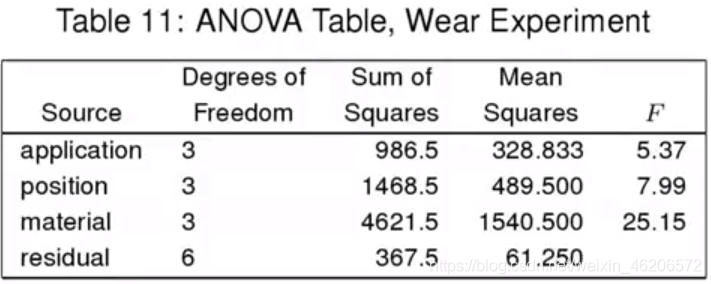

其中F统计量
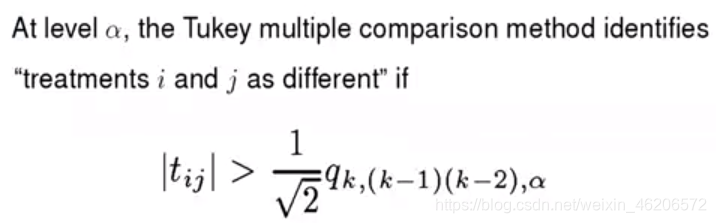
结果分析
P值
位置：P(F3.6 > 5.37) = 0.039
应用：P(F3.6 > 7.99) = 0.016
P值 < 0.05，说明两区组因子有影响

4种处理方法的差异：P(F3.6 > 25.15) = 0.0008
说明四种处理方法有差异

自由度：k=4，(k-1)(k-2)=6
Tukey多重比较法在0.05水平下的临界值为3.46（计算方法如下）。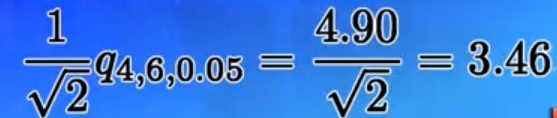
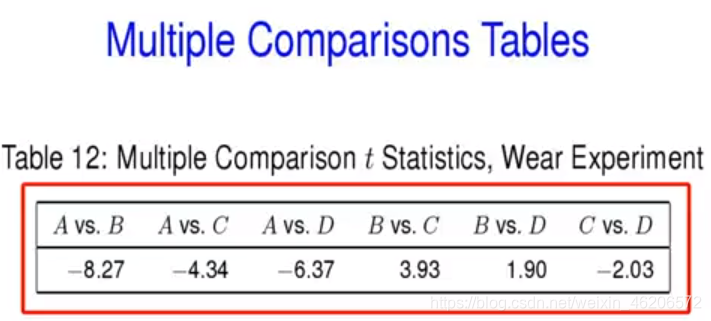
在这里插入图片描述

分析：绝对值与3.46相比，前4个大，显著；后2个小，不显著。

忽略区组影响的方差分析表：没影响才忽略

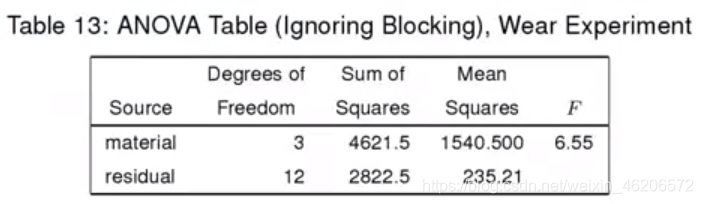
忽略区组： P(F3,12 > 6.55) = 0.007
不忽略区组： P(F3,6 > 25.15) = 0.008

（三）正交（希腊）拉丁方设计：多个区组因子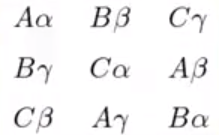
在这里插入图片描述
模型：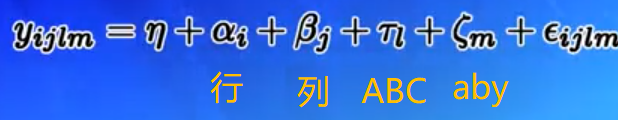

方差分析表

超希腊拉丁方：多个正交拉丁方叠加

（五）平衡不完全区组设计BIBD

不完全区组的必要条件：处理 t > 区组k，每对处理出现相同的个数

例5：5种轮胎放在需4个轮胎的车上
例6：品尝冰淇淋，味蕾能力有限，只能感觉 k 种
例7：品酒师品10种酒，肚子有限喝不下太多

例8：轮胎耐磨试验：4种轮胎3种材料
相同点：处理两两间配对只出现2次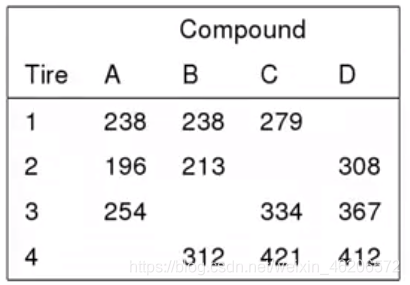
在这里插入图片描述

（k-1）个与其配对

模型
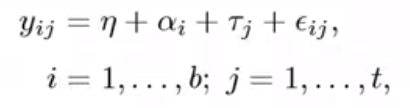
处理和
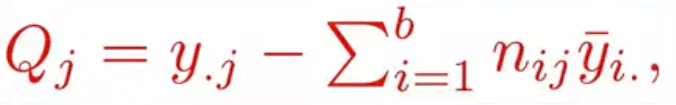
方差分析表
多重比较

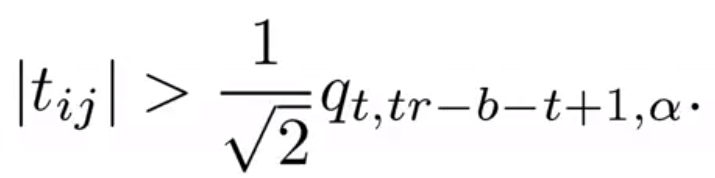
续例8：

P(F3.5 > 37.24) = 0.0008
P(F3.5 > 19.73) = 0.0034

在0.05水平下，AB 与 CD 有显著差异