一、什么是算法?
算法(Algorithm)是用于解决特定问题的一系列的执行步骤,算法代表着用系统的方法描述解决问题的策略机制。也就是说,能够对一定规范的输入,在有限时间内获得所要求的输出。如果一个算法有缺陷,或不适合于某个问题,执行这个算法将不能解决这个问题。不同的算法可能用不同的时间、空间和效率来完成同样的任务。
二、如何评判算法的好坏?
解决同一个问题可以有多种不同的算法,而算法优劣将直接影响程序的执行效率。一个算法的优劣可以用空间复杂度与时间复杂度来衡量。
1、时间复杂度
时间复杂度(time complexity)是指执行算法所需要的计算工作量。一般用大O表示法来描述复杂度,它表示的是数据规模 n 对应的复杂度。
计算一个算法的时间复杂度一般会忽略常数、系数和低阶,对数阶一般省略底数。如:
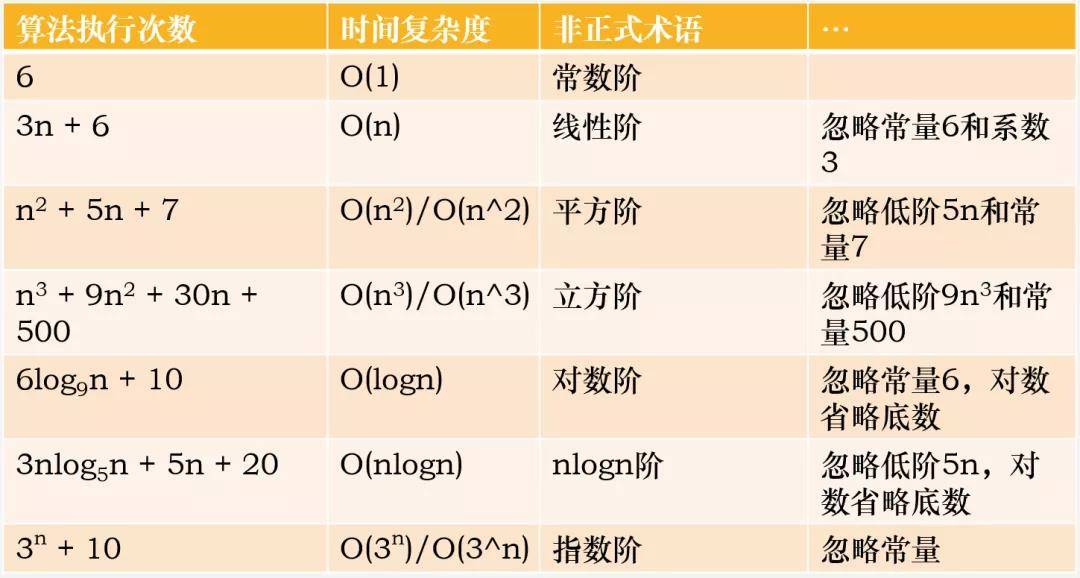
从上图中,我们可以看到当 n 的值很小时,时间复杂度之间不易区分,很难说谁处于主导地位,但是当 n 不断增大时,我们就能看到很明显的区别,谁处于主导地位就一目了然:O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(3^n)
(1) 如下三行代码 n = n * n ; m = 2 * m ; int k = m + n ; 执行的次数均为 1,所以该程序段的执行时间是一个与问题规模n无关的常数。算法的时间复杂度为常数阶,记作 O(1)。如果算法的执行时间不随着问题规模n的增加而增长,即使算法中有上千条语句,其执行时间也不过是一个较大的常数。此类算法的时间复杂度是O(1)。
public void testMethod(int n , int m){n = n * n;m = 2 *m;int k = m + m;}
(2) 如下代码第一个循环执行 k 次,第二个循环执行 m 次 ,所有该算法的时间复杂度为 O(m+k) = O(n)。
public void testMethod(int m ,int k){//第一个循环for(int i = 0 ; i < k ; i++){System.out.println(i);}//第二个循环for(int j = 0 ; j < m ; j++){System.out.println(j);}}
(3) 如下代码一个for循环的时间复杂度为 Ο(n),第二个for循环的时间复杂度为 Ο(n^2),则整个算法的时间复杂度为Ο(n+n^2)=Ο(n^2)。
public void testMethod(int n){//第一个循环for(int i = 0 ; i < n ; i++){System.out.println(i);}//第二个循环for(int j = 0 ; j < n ; j++){//子循环for(int k = 0 ; k < n ; k++){System.out.println(j*k);}}}
(4) 如下代码 int i = 1;只执行一次,i = i * 2;需要执行  次,所以时间复杂度为O(logn)。
次,所以时间复杂度为O(logn)。
public void testMethod(int n){int i = 1;while(i < n){i = i * 2;}}
(5) 如下代码是我们熟知的冒泡排序。从代码中可以看出内层循环体一共了执行了 (n-1) + (n-2) + (n-3) … + 2 + 1 = n * (n-1) / 2 = 0.5 * n ^ 2 - 0.5 * n 次,那么时间复杂度是 O(n^2)。
// 冒泡排序--升序public void bubbleSort(int[] arr) {int n = arr.length;//数组长度// 外层循环n - 1 ,控制轮数for (int i = 0; i < n - 1; i++) {// 内层循环 N - 1 - i,控制每轮比较的次数for (int j = 0; j < n - 1 - i; j++) {// 两两相比,小靠前if (arr[j] > arr[j + 1]) {int temp = arr[j];// 定义一个临时变量,存储arr[j]的值arr[j] = arr[j + 1];arr[j + 1] = temp;}}}}
2、空间复杂度
空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度,记作S(n)。空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度。
一个算法在计算机存储器上所占的存储空间分为三个部分,分别是:存储算法代码本身的存储空间、存储算法输入输出数据所占用的存储空间和算法执行过程中需要临时存储的数据所占用的空间。
存储算法输入输出数据所占用的存储空间是由要解决的问题决定的,它不会随着算法的不同而改变;存储算法代码本身所占的存储空间与代码是否精简有关,要节省这一部分存储空间,必须写出较短的代码;算法在运行过程中临时占用的存储空间随算法的不同而异,有的算法只需要占用少量的临时工作单元,而且不随问题规模的大小而改变,我们称这种算法是“就地\"进行的,是节省存储的算法,有的算法需要占用的临时工作单元数与解决问题的规模n有关,它随着n的增大而增大,当n较大时,将占用较多的存储单元,例如快速排序和归并排序算法就属于这种情况。

