Transform
CSS3中,
transform属性允许盒子模型被进行二维或三维空间坐标的变换。使用该属性之后,元素主要可以进行以下变换:
- 旋转(rotate)
- 平移(translate)
- 缩放(scale)
- 倾斜(skew)
下面的图片我们实现了一个旋转和缩放的变换、然后结合animation属性实现了一种常见的动画效果。
Transform API
通过文章开头介绍的几种变换,我们可以简单概括为:
| 属性 | 描述 | demo |
|---|---|---|
| translate(x,y) | 平移变换 [注意 x,y有单位] | 测试 |
| scale(x,y) | 缩放变换 [x,y无单位] | 测试 |
| rotate(angle) | 旋转变换[单位为弧度,deg] | 测试 |
| skew(angleX,angleY) | 拉伸变换[单位为弧度,deg] | 测试 |
| matrix(a,b,c,d,e,f) | 变换矩阵[重点] | 测试 |
基本的用法现在网上都能查询到,这里就不再赘述了。下面主要讲一下matrix。
Matrix
中文译为”矩阵”,在本文中可以理解为transform模板函数。那么矩阵到底有什么用呢?相信大家都在大学或多或少了解过线代,我所理解的矩阵它的本质就是线性方程组,通过建立一种对应关系,得到目标结果的一种工具。
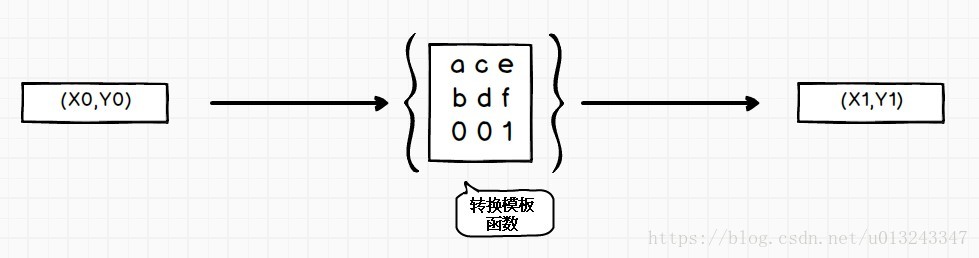
下图是一个矩阵方程,它的作用就是将原有坐标值(X0,Y0)通过某种变换,转换目标值(X1,Y1)。
那么,matrix和transiform之间有什么联系?
通过了解到矩阵的作用,那么我们可以想象,所谓的transform变换就是一系列的坐标值转换。
假设有一种模板矩阵, 它的功能就是将我们原有的坐标值,通过模板矩阵的处理,实现平移、旋转、缩放、拉伸等效果的转换过程。
简单的概括就是,我想要实现一个平移的效果。只需要实现三个步骤即可:
- 初始化一个图形
- 创建一个模板矩阵
- 将模板矩阵应用到初始化图形中
matrix 模板矩阵
下面是常见的几个矩阵模板:
| 属性 | 描述 | demo |
|---|---|---|
matrix(1, 0, 0, 1, e, f) |
平移 | 测试 |
matrix(a, 0, 0, d, 0, 0) |
缩放 | 测试 |
matrix(cosθ,sinθ,-sinθ,cosθ,0,0) |
旋转 | 测试 |
matrix(1,tan(θy),tan(θx),1,0,0) |
拉伸 | 测试 |
再进一步学习之前,先来回顾一些基础线代知识:
矩阵乘法
计算规则是,第一个矩阵第一行的每个数字(a和b),各自乘以第二个矩阵第一列对应位置的数字(1和2),然后将乘积相加( a x 1 + b x 2),得到结果矩阵左上角的那个值a+2b。
平移(translate)
数学意义是:
其中,(x0,y0)为起始点坐标,(x1,y1)就是我们要输出的目标坐标值。
不难发现,e,f就是我们想要的横纵坐标上的偏移量。
从上面的矩阵公式。我们得出,通过模板矩阵相乘,就可以得到目标函数的坐标值。
思考题:为什么坐标值格式会是(x,y,1),而不是(x,y)呢。这个1代表的是什么?
缩放(scale)
有了上面的铺垫,下面的缩放就比较简单了。
首先想一想,缩放的原理是什么?
缩放就是将x,y在对应横纵轴上进行等比例的伸长或缩小。
数学意义:
a, d 就是横纵坐标的伸缩量。
思考题:为什么b,c会设置为0?
旋转(rotate)
[注意] 本文仅介绍绕原点的二维旋转。
旋转变换就明显与上面的两种有质的飞跃了,因为前两种只是单纯的线性变换,旋转变换就加上了一种新的因素(弧度)。
数学意义:
v绕原点旋转θ 角,得到点v’,假设 v点的坐标是(x, y) ,那么可以推导得到 v’点的坐标(x’, y’)(设原点到v的距离是r,原点到v点的向量与x轴的夹角是ϕ )
[拓展] 旋转矩阵的推导原理:
- 首先是(x0,y0)关于弧度的表达式:
- (x1,y1)关于弧度的表达式:(1式)
展开上面的三角函数,(2式)
- 将1式代入到2式,得
拉伸(skew)
拉伸变换也可以称为倾斜变换或斜切变换。
数学意义:
倾斜的意义就是在于原点是一个动态值,然后再绕水平或竖直方向进行一定角度的倾斜。效果就类似于拉伸一个弹性物体。
思考题:自行推导一下。
tips:
好了,基本的图形变换的数学原理已经讲完了,以后还有后续的公式来进行扩充。谢谢~