平衡二叉搜索树
平衡二叉搜索树(Self-balancing binary search tree)又被称为AVL树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。 数值关系,右孩子的值 > 当前节点的值 > 左孩子的值。
平衡二叉搜索树节点的状态
1:左子树比右子树高 LH
2:左子树和右子树一样高 EH
3:右子树比左子树高 RH

如上图每个节点的状态如下。

TreeNode 的定义
static final class TreeNode<T> {
TreeStatus treeStatus = TreeStatus.EH;
T value;
TreeNode<T> left;
TreeNode<T> right;
TreeNode<T> parent;
public TreeNode(T value) {
this.value = value;
}
public TreeNode(T value, TreeNode<T> p) {
this.value = value;
this.parent = p;
}
public String toString() {
return "value=" + value.toString();
}
}
搜索插入点
以向平衡二叉树插入105为例。
搜索过程
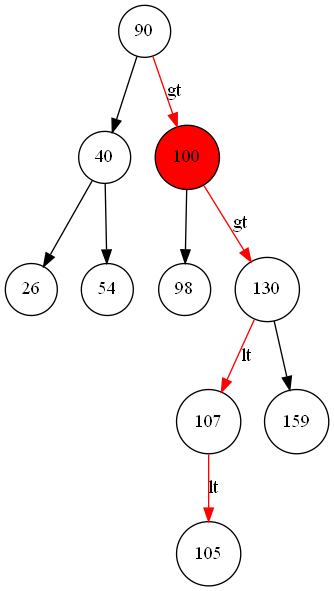
105 gt 90 搜索90的右子树
105 gt 100 搜索100的右子树
105 lt 130 搜索130的左子树
105 lt 107 搜索107的左子树
107的左子树为空,停止搜索, 105为107的左孩子。
插入新点节之后搜索途中的节点的状态发生改变,需要回溯更改每个节点的状态。
107节点的状态为EH,105为107的左孩子,所以107的状态更改为LH,
130节点的状态为EH,107为130的左孩子,所以130的状态更改为LH,
100节点的状态为RH, 130 为100的右孩子, 所以 100节点失去平衡。
向上回溯的图解如下。
情况1: 回溯途中所有节点的状态都为EH, 那么树的平衡性不会发生改变。

直观一点的图。

向上回溯的路径为:

在插入54节点之前,所有节点的状态为EH,但是在插入54节点之后。
51 由EH---> RH
55 由EH--->LH
50 由EH---> RH
100 由EH--->LH
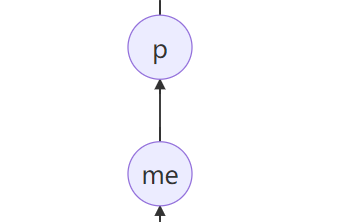
如果me是p的左孩子,那么p的状态改为LH,
如果me是p的右孩子,那么p的状态改为RH。
p=p.parent ;
me=me.parent;
情况2:回溯的途中遇到了第一个状态不为EH的节点,假设该节点为pp。

由pp,p来决定pp树是否失去平衡。
假设pp的状态为LH,
如果p为pp的左孩子,那么pp树将会失去平衡。 如果p的状态为LH,那么进行LL旋转,如果p的状态为RH,那么进行LR旋转。
如果p为pp的右孩子,那么pp树将维持平衡,并且pp的状态需要修改为EH.

平衡二叉树有6个插入点:

当插入点为1或者2时, 引起LL旋转。
当插入点为3或者4时,引起LR旋转。
当插入点为5或者6时,不会引发旋转。
由(pp.treeStatus, p.treeStatus)来决定做那种旋转。。。
镜像的pp的状态为RH;
下面开始讲旋转:
LL 旋转
pp为失衡的节点。 p为pp的左孩子,me为p的左孩子, xpp为pp的父节点。
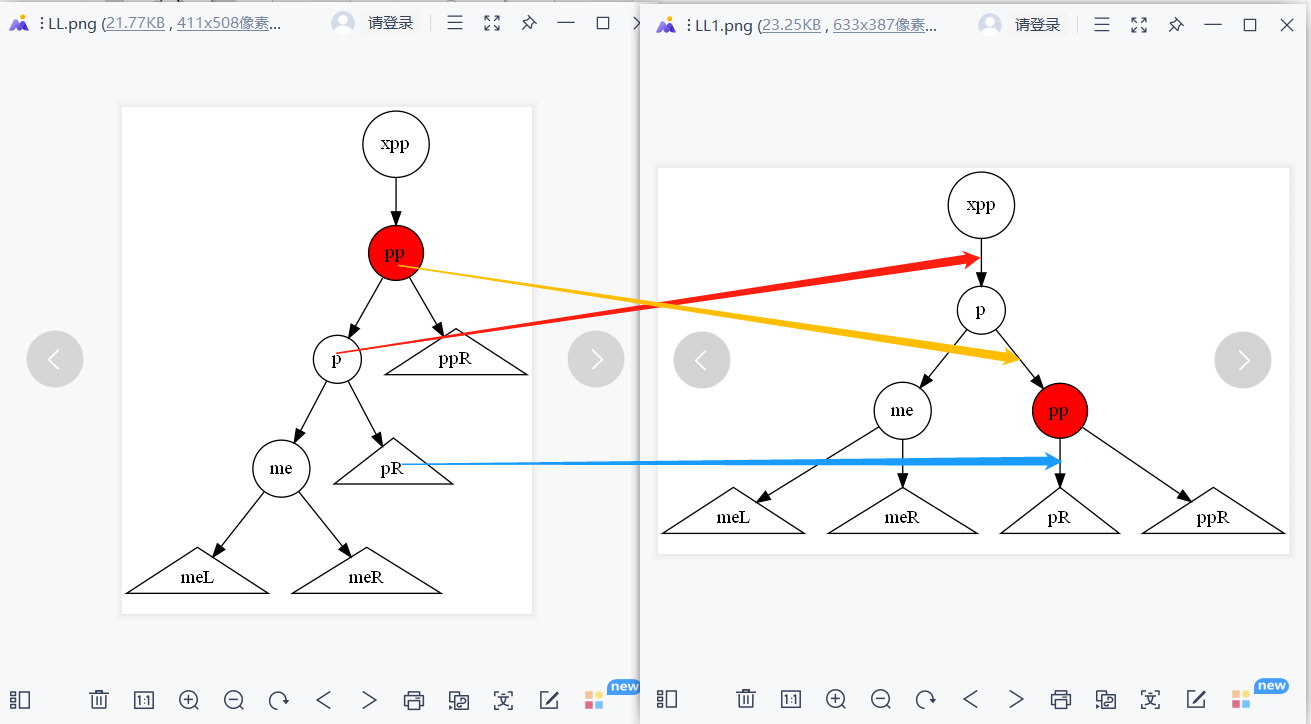
步骤1: pr = p.right;
步骤2: p.pright = pp; pp.parent = p;
步骤3: pp.left = pr ; pr.parent = pp ;
步骤4: p.parent=xpp , 确定p是xpp的左孩子还是右孩子
重点说明 如果xpp为空,则p节点为新的root节点。
旋转之后 p和pp节点的状态均为EH。
LR旋转
pp为失衡的节点。 p为pp的左孩子,me为p的右孩子, xpp为pp的父节点。

步骤1 : mel =me.left; mer= me.right
步骤2: me.left = p ; me.right = pp; p.parent = me, pp.parent = me ;
步骤3: p.right = mel ; pp.left = mer ; mel.parent = p ; mer.parent = pp ;
步骤4: me.parent = xpp ; 确定me是xpp的左孩子还是右孩子
重点说明 如果xpp为空,则me节点为新的root节点。
状态的改变:
如果me的状态为LH 那么p的状态为EH , pp的状态为RH;
如果me的状态为RH 那么p的状态为LH, pp的状态为EH ;
如果me的状态为EH 那么p的状态为EH , pp的状态为EH;
旋转完成之后me的状态一定为EH。
RR旋转和LL旋转是镜像关系。

RL和LR是镜像关系。
如何检测构造的树是正确的?
当树的节点数量很少时,使用人眼进行观察验证可行,但如果树的节点数量增多时,很明显使用人眼观察这种方法是不行的。
这部分涉及到循环不变式理论,具体来说就是实现一个方法来检测构造的树是正确的,如HashMap中的checkInvariants方法,用来检测构造的树是否满足红黑树的约束。

类似的为了证明自己写的代码是正确的,这需要使用循环不变式来进行自我证明。 当然也可以按照这种检测法制来实现一个方法来检测别人写的代码是否正确。
private boolean checkInvariants(TreeNode<T> t) {
if (t == null) {
return true;
}
if (t == root && t.parent != null) {
return false;
}
TreeNode<T> l = t.left;
TreeNode<T> r = t.right;
// 都等于空时 t 的状态应该为EH
if (l == null && r == null) {
if (t.treeStatus != TreeStatus.EH) {
return false;
}
return true;
}
// 左为空,右不为空
if (l == null && r != null) {
if (r.parent != t) {
return false;
}
if (t.treeStatus != TreeStatus.RH) {
return false;
}
if (r.left != null || r.right != null) {
return false;
}
if (compare(r.value, t.value) <= 0) {
return false;
}
return true;
}
// 右为空,左不为空
if (r == null && l != null) {
if (l.parent != t) {
return false;
}
if (t.treeStatus != TreeStatus.LH) {
return false;
}
if (l.left != null || l.right != null) {
return false;
}
if (compare(l.value, t.value) >= 0) {
return false;
}
return true;
}
// 都不为空
boolean fl = checkInvariants(l);
if (fl == false) {
return false;
}
boolean fr = checkInvariants(r);
if (fr == false) {
return false;
}
if (compare(l.value, t.value) >= 0 || compare(t.value, r.value) >= 0) {
return false;
}
int lh = getH(l);
int rh = getH(r);
if (t.treeStatus == TreeStatus.EH) {
return (lh == rh);
} else if (t.treeStatus == TreeStatus.RH) {
return (rh - lh) == 1;
} else {
return (lh - rh) == 1;
}
}
static <T> int getH(TreeNode<T> node) {
int i = 0;
while (node != null) {
if (node.treeStatus != TreeStatus.RH) {
node = node.left;
} else {
node = node.right;
}
i++;
}
return i;
}
精简版循环不变式
private boolean checkInvariants(TreeNode<T> t) {
if (t == null) {
return true;
}
if (t == root && t.parent != null) {
return false;
}
TreeNode<T> l = t.left;
if (l != null && (l.parent != t || !checkInvariants(l) || compare(l.value,t.value) >=0)) {
return false;
}
TreeNode<T> r = t.right;
if (r != null && (r.parent != t || !checkInvariants(r) || compare(r.value, t.value) <= 0)) {
return false;
}
int lh = getH(l);
int rh = getH(r);
if (t.treeStatus == TreeStatus.EH) {
return (lh == rh);
} else if (t.treeStatus == TreeStatus.RH) {
return (rh - lh) == 1;
} else {
return (lh - rh) == 1;
}
}
前者代码多,但是执行效率稍微高一点。


